| Nộp bài | Các bài nộp | Làm tốt nhất | Về danh sách bài |
STABLE - Ổn định |
Trong mạng xã hội, mỗi trang web được tổ chức trên một máy tính thành viên và cung cấp dịch vụ truy nhập tới một số trang web khác. Để truy nhập tới một trang web nào đó không có trong danh mục kết nối trực tiếp của mình, người dùng phải truy nhập tới trang web khác có kết nối với mình, dựa vào danh mục dịch vụ của trang web này để chuyển tới trang web khác theo tùy chọn, cứ như thế cho đến khi tới được trang web mình cần. Thời gian để truy nhập tới một trang web phụ thuộc chủ yếu và số lần mở trang web trong quá trình truy nhập. Như vậy, người dùng cần chủ động chọn lộ trình truy nhập hợp lí.
Sau một thời gian làm việc trên mạng, Sáng - một thành viên nhiệt thành đã tích lũy kinh nghiệm, tạo một cơ sở dữ liệu, cho biết từ một trang web có thể đi tới những trang web nào trong mạng. Trong cơ sở dữ liệu, các trang web được đánh số từ 1 đến n và có m bản ghi, mỗi bản ghi có dạng cặp có thứ tự (u, v) cho biết trang web u có kết nối tới trang web v ( 1 ≤ u, v ≤ n, u ≠ v). Cơ sở dữ liệu chưa được chuẩn hóa, vì vậy có thể chứa các cặp (u, v) giống nhau.
Trang web của Sáng có số hiệu là s. Dựa vào cơ sở dữ liệu, Sáng có thể xác định lộ trình truy nhập nhanh nhất (tức là số lần phải mở trang web là ít nhất) từ trang web s tới trang web u bất kì. Tuy vậy, ở mạng xã hội, mọi chuyện đều có thể xảy ra: một khu vực nào đó bị mất điện, máy của một thành viên bị hỏng, trang web đó đang bị đóng để nâng cấp, ... Kết quả là một vài trang web nào đó có thể tạm thời không hoạt động. Như vậy, nếu từ s có ít nhất hai lộ trình nhanh nhất khác nhau tới u thì khả năng thực hiện truy nhập được một cách nhanh nhất tới u là lớn hơn so với những trang web chỉ có duy nhất một lộ trình nhanh nhất. Hai lộ trình gọi là khác nhau nếu có ít nhất một trang web có ở lộ trình này mà không có ở lộ trình kia hoặc cả hai lộ trình cùng đi qua những trang web như nhau nhưng theo các trình tự khác nhau. Những trang web mà từ s tới đó có ít ra là hai lộ trình nhanh nhất khác nhau được gọi là ổn định đối với s. Trang web mà từ s không có lộ trình tới nó là không ổn định đối với s.
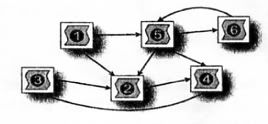
Ví dụ, với mạng nêu ở hình trên (n = 6, m = 9) các trang web 4 và 3 là ổn định với s = 1 (từ 1 tới 4 có 2 lộ trình nhanh nhất: 1 - 2 - 4 và 1 - 5 - 4, từ 1 tới 3 cũng có 2 lộ trình nhanh nhất: 1 - 2 - 4 - 3 và 1 - 5 - 4 - 3).
Yêu cầu
Cho các số nguyên dương n, m, s và m cặp số (u, v) xác định từ u có thể kết nối trực tiếp tới được v. Hãy xác định số lượng trang web ổn định đối với s.
Dữ liệu
- Dòng đầu tiên chứa 3 số nguyên n, m và s (2 ≤ 10000, 1 ≤ m ≤ 50000, 1 ≤ s ≤ n).
- Mỗi dòng trong m dòng tiếp theo chứa 2 số nguyên u và v (1 ≤ u, v ≤ n, u ≠ v).
Các số trên một dòng được ghi cách nhau ít nhất một dấu cách.
Kết quả
Một số nguyên - số trang web ổn định đối với s.
Ví dụ
(giống ví dụ nêu trong đề bài, nhưng có chứa các cặp dữ liệu lặp)
Input: 6 11 1 1 5 1 5 5 6 1 2 5 4 2 4 4 3 5 4 5 2 3 2 6 5 Output: 2
| Được gửi lên bởi: | Lê Đôn Khuê |
| Ngày: | 2010-03-11 |
| Thời gian chạy: | 0.200s |
| Giới hạn mã nguồn: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Ngôn ngữ cho phép: | Tất cả ngoại trừ: GOSU NODEJS OBJC PERL6 PYPY RUST SED SQLITE VB.NET |
| Nguồn bài: | VOI 2010 |
hide comments
|
||||||||
|
2021-05-27 18:03:52
Tham khảo: https://vnspoj.github.io/problems/STABLE |
||||||||
|
2020-04-11 10:22:23
WTF bai nay cai so thuc de lam gi |
||||||||
|
2018-12-05 09:11:05
bạn nào làm đếm số đường đi ngắn nhất từ s đến u thì thử test 4 4 1 1 2 1 3 2 4 3 4 số cách đi từ 1 đến 4 là 2, giả sử nhân đồ thị này lên 3000 lần, nối đuôi nhau, thì số cách đi lên tới tận 2^3000 |
||||||||
|
2017-10-02 10:31:21
Ahihi em cung de kieu so thuc moi AC Ai do giai thich giup em voi... Last edit: 2017-10-02 10:38:59 |
||||||||
|
2017-10-02 10:01:06
xin chào các fan hâm hộ :))))))))))) |
||||||||
|
2017-10-02 09:57:46
i am nguyễn văn bang |
||||||||
|
2017-09-19 04:20:43
Nên kiểm tra nút ổn định = bool thay vì int :) |
||||||||
|
2017-08-24 20:46:47
chời địu -.- cạn mẹ lời bài phải để số thực ms AC chứ để int64 tràn số :v lm ngồi debug cả buổi :'( |
||||||||
|
2017-08-18 15:54:30
kham khảo: https://vietcodes.github.io/code/48/ |
||||||||
|
2017-08-15 11:23:45
THAM KHẢO THUẬT TOÁN, CODE TẠI: http://yeulaptrinh.pw/1012/stable-spoj/ |
||||||||

 RSS
RSS